Хохирогчдын хувьд махчин амьтдыг эсэргүүцэх зорилгоор боловсруулсан дасан зохицолт нь эдгээр дасан зохицох чадварыг даван туулах махчин механизмыг хөгжүүлэхэд хувь нэмэр оруулдаг. Махчин амьтан, хохирогчдын урт удаан хугацаанд оршин тогтнох нь судалгааны талбайд хоёуланг нь тогтвортой хадгалдаг харилцан үйлчлэлийн тогтолцоог бий болгоход хүргэдэг. Ийм системийг зөрчих нь хүрээлэн буй орчны сөрөг үр дагаварт хүргэдэг.
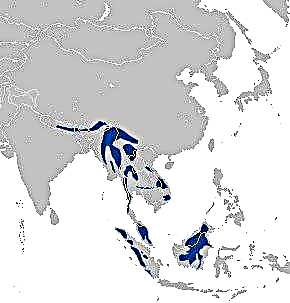
Хувьслын эволюцийн харилцааг зөрчих сөрөг үр дагавар нь зүйлийг нэвтрүүлэх явцад ажиглагддаг. Ялангуяа Австралид нэвтрүүлсэн ямаа, туулай нь энэ тивд элбэг дэлбэг байх хяналтын механизм байдаггүй бөгөөд энэ нь байгалийн экосистемийг устгахад хүргэдэг.
Математик загвар
Хоёр зүйлийн амьтад тодорхой нутаг дэвсгэрт амьдардаг гэж бодъё: туулай (ургамал тэжээх), үнэг (туулайгаар хооллох). Туулай х < displaystyle x>, үнэгний у < displaystyle y> тоог гарга. Мальтус загварыг шаардлагатай нэмэлт өөрчлөлтөөр ашиглан үнэгээр туулай идэж байгааг харгалзан Вольтерра моделийн нэрийг агуулсан дараах системд хүрлээ.
<x ˙ = (α - c y) x, y ˙ = (- β + d x) y байна. < displaystyle < эхэлнэ Энэ систем нь туулай, үнэгний тоо тогтмол байх үед тэнцвэрт байдалд ордог. Энэ төлөвөөс хазайх нь гармоник осцилляторын хэлбэлзэлтэй төстэй туулай, үнэгний тоо хэлбэлзэлд хүргэдэг. Гармоник осцилляторын хувьд энэ зан чанар нь тогтвортой биш юм: загварт бага зэрэг өөрчлөлт орох (жишээлбэл, туулайнд шаардагдах хязгаарлагдмал нөөцийг харгалзан үзэх нь) нь зан чанарт чанарын өөрчлөлтөд хүргэдэг. Жишээлбэл, тэнцвэрт байдал тогтвортой болж, тоонуудын хэлбэлзэл буурах болно. Тэнцвэрийн байрлалаас ямар нэгэн жижиг хазайлт нь аль нэг зүйлийн бүрэн устах хүртэл сүйрлийн үр дагаварт хүргэдэг бол эсрэг нөхцөл байдал бас боломжтой. Эдгээр хувилбаруудаас аль нь хэрэгжиж байгаа талаар асуухад Вольтерра-Трэй загвар нь хариулт өгөхгүй байна: энд нэмэлт судалгаа хийх шаардлагатай байна. Осцилляцийн онолын үүднээс авч үзвэл Вольтерра - Лотка загвар нь хөдөлгөөний анхны интегралтай консерватив систем юм. Энэ систем нь бүдүүлэг биш юм, учир нь тэгшитгэлийн баруун талд бага зэрэг өөрчлөлт нь түүний динамик зан чанарт чанарын өөрчлөлтөд хүргэдэг. Гэсэн хэдий ч тэгшитгэлийн баруун талыг "бага зэрэг" өөрчлөх боломжтой бөгөөд ингэснээр систем өөрөө эргэлдэх болно. Барзгар динамик системд хамаарах тогтвортой хязгаарлалтын мөчлөг байгаа нь тухайн загварыг ашиглах талбайн мэдэгдэхүйц өргөжихөд хувь нэмэр оруулдаг. Махчин амьтан, тэдний хохирогчдын бүлгийн амьдралын хэв маяг нь загварын зан чанарыг эрс өөрчилдөг бөгөөд энэ нь тогтвортой байдлыг нэмэгдүүлдэг. Үндэслэл: бүлгийн амьдралын хэв маягаар бол боломжит хохирогчидтой махчин амьтдын санамсаргүй уулзах давтамж буурч байгаа нь Серенгети парк дахь арслан, хээрийн бүсийн тоонуудын динамикийн ажиглалтаар нотлогдож байна. Хоёр төрлийн биологийн зүйл (популяци) хосолсон загварыг Волтерра - Лотка загвар гэж нэрлэдэг. Үүнийг анх 1925 онд Альфред Лотка олж авсан (харилцан үйлчлэх биологийн популяцийн динамикийг тодорхойлоход ашигладаг). 1926 онд (Лоткагаас үл хамааран) ижил төстэй (мөн илүү төвөгтэй) загваруудыг Италийн математикч Вито Вольтерра боловсруулжээ. Түүний хүрээлэн буй орчны асуудлын талаархи гүнзгий судалгаа нь биологийн олон нийтийн (математик экологи) математикийн онолын үндэс суурийг тавьсан юм.Загварын зан байдал
Түүх